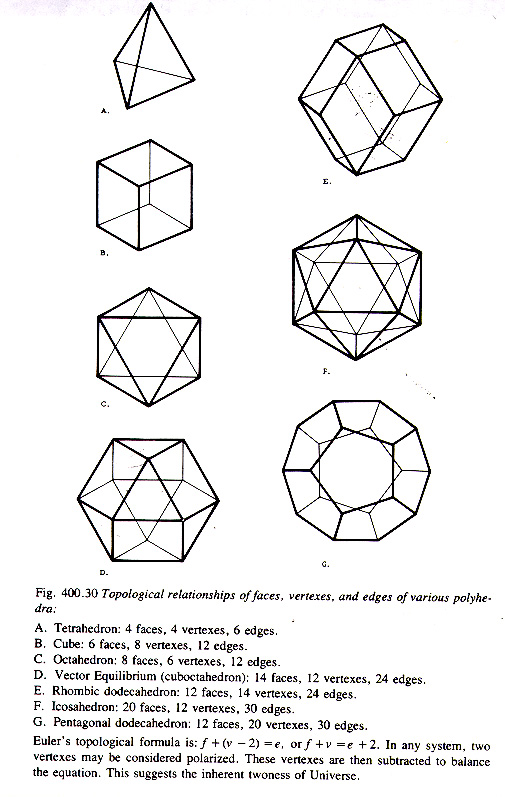
Plato, the ancient Greek, spoke of the 5 regular perfect solids noted by antiquity. They are shown below as items A,B,C,G, and F. They are called:

A) TETRA (FOUR) HEDRON (SIDES)

B) HEXA (SIX) HEDRON (SIDES) (MORE COMMONLY CALLED A CUBE)

C) OCTA (EIGHT) HEDRON (SIDES)

G) PENTAGONAL (PENTA = 5, GON = ANGLE; THEREFORE EACH FACE OF THIS POLYHEDRON HAS FIVE ANGLES) DODECA (TWELVE) HEDRON

F) ICOSA (TWENTY) HEDRON

Also shown are two other fundamental shapes, one of which is semiregular and the other irregular: the cuboctahedron (renamed by Bucky the vector equilibrium--note that the cuboctahedron is like a combination of an exploded cube and octahedron (it has the six square sides of a cube plus the 8 triangular sides of an octahedron); hence the name) and the rhombic dodecahedron.

5 and only 5 regular perfect (formed only of one type of polygon) solids can exist. Each face of a regular (where each edge length is identical) solid must be made of at least 3 sides, as in a regular equilateral triangle, and at most 5 sides, as in a pentagon. The reason why this is so is because, obviously, in order for a polyhederon to close back on itself, the vertex junction where the polygons meet cannot be equal to or exceed 360 degrees. Further, equally obvious, at least 3 polygons must meet at a junction in building a polyhedron.

3 triangles, 4 triangles and 5 triangles can meet this criterion: the sum of angles meeting at a vertex junction are: 180 degrees, 240 degrees, and 300 degrees, but since 6 times 60 equals 360, triangles cannot be used further in building multidimensional polyhedra. These three instances describe, respectively, the tetrahedron, octahedron, and icosahedron.

Next are squares with 4 sides--and only 3 can meet to add up to 270 (3 times 90) degrees at a junction; 4 would again yield the limit number of 360. Next we have pentagons, and again, only 3 can meet for similar reasons. At hexagons, which have 6 sides, we have reached the limit--each hexagon has a vertex angle of 120 degrees, and even 3 yield the limit number of 360, such that hexagons cannot be used only with themselves to close a polyhedron. All remaining polygons will have vertex angles greater than 120 degrees, so 5 and only 5 platonic solids shall ever exist.

Also of note is the phenomenon of duals. Two polyhedra are said to be duals if the defining information of one suggests the defining information of the other. In each case of duals, therefore, we will see that the number of vertices in the first dual equals the number of faces of the other dual, while the number of edges is the same. In the above image, we see 4 families: the tetrahedron family; the cube and octahedron family; the pentagonal dodecahedron and the icosahedron family; and the vector equilibrium and rhombic dodecahedron family. Note also that in the first three families, if you place dots in the exact center of each face, and connect the lines, you will automatically form the dual of the original.